These models are used to determine the economic value of derivative financial assets in relation to their returns and risk. Thus, option valuation theory has been used to carry out valuations of debt securities, warrants or even patents, among many others. Among the many valuation models, the best known is the following:
Black and Scholes Model
This is a financial mathematics methodology created by Robert C. Merton following the Black and Scholes studies developed in 1973 by Fisher Black and Myron Scholes.
Black-Scholes is a pricing model used to determine the fair price or theoretical value of a call or put option as a function of six variables, such as volatility, option type, underlying stock price, time, strike price and risk-free rate.
Assumptions of the Black-Scholes-Merton model:
Lognormal distribution: The Black-Scholes-Merton model assumes that stock prices follow a lognormal distribution (a continuous probability distribution that describes situations in which the logarithm of a random variable follows a normal distribution) based on the principle that asset prices cannot take a negative value; they are bounded by zero.
No dividends: The BSM model assumes that stocks do not pay dividends or yields.
Expiration date: The model assumes that options can only be exercised on their expiration or maturity date. Therefore, it does not accurately value American options. It is widely used in the European options market.
Random walk: The stock market is very volatile, so a random walk state is assumed, since the direction of the market can never really be predicted.
Frictionless market: In the BSM model it is assumed that there are no transaction costs, including commissions and brokerage.
Risk-free interest rate: Interest rates are assumed to be constant, so the underlying asset is risk-free.
Normal distribution: Stock returns are normally distributed. This implies that market volatility is constant over time.
No arbitrage: There is no arbitrage. It avoids the opportunity to make a risk-free profit.
As for the calculation, the Black-Scholes theory model uses a rather complex formula to define the fair price that the call options should have. Therefore, it is best to opt for some kind of simulator that allows us to know the data without having to perform the complex operation on our own. In any case, the calculation formula is detailed as follows:
The Black-Scholes-Merton formula for a call option is:

Where:
– C(S0, t, K, r, σ) = is the call option price.
– S0 = is the current price of the underlying asset
– t = is the time remaining until expiration of the option
– K = is the strike price of the option
– r = is the risk-free interest rate
– σ = is the volatility of the underlying asset
– N(d1) and N(d2) = are the cumulative normal distribution functions.
The Black-Scholes-Merton formula for a put option is:
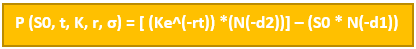
Where:
– P(S0, t, K, r, σ) = is the price of the put option.
The values of d1 and d2 are calculated as follows:

It is important to keep in mind that the Black-Scholes-Merton formula is a theoretical model and does not take into account all the factors that can affect the price of an option.
(Fernández, IESE. (1997). UTILIZACIÓN DE LA FÓRMULA DE BLACK Y SCHOLES PARA VALORAR OPCIONES; https://web.iese.edu/PabloFernandez/docs/FN-0425.pdf )
